Table of Contents
- 1. Preface
- 2. Introduction
- 3. Geometries
- 4. Changing the sampling
- 4.1. Introduction
- 4.2. Sampler interface
- 4.3. Concrete sampler classes
- 5. Scoring
- 5.1. Introduction
- 5.2. The scoring framework
- 5.3. Standard scoring
- 5.4. Advices for scoring
- 6. Importance sampling
- 7. Weight window technique
- 8. Weight roulette
- 8.1. Introduction
- 8.2. The weight roulette concept
This document gives short descriptions of the basic concepts of the implementation of scoring and importance sampling (or geometrical splitting and Russian roulette) in Geant4. The reader is expected to be familiar with both Geant4 and the concept of importance sampling.
The scoring implemented intends to appraise particle quantities primarily for checking importance sampling and it applies to "cells" (physical volumes or replicas) of a given geometry. The design highly supports customization. Nevertheless a standard scoring implementation for quantities interesting for importance sampling such as: tracks entering a cell, average track weight, energy averaged in different ways, collisions inside the cell is provided.
Importance sampling and weight roulette are variance reduction techniques. The purpose of variance reduction is to save computing time.
Therefore geometrical importance sampling (also called geometrical splitting and Russian roulette) sample particle histories entering important regions more often and histories entering less important regions less often.
Weight roulette (also called weight cutoff) is used if importance sampling together with another variance reduction technique called implicit capture are applied. It reduces the number of particles with a weight to low to contribute much to the result.
Comparing the result of a variance reduced simulation to an analogue sampled simulation the mean value must be equal while the variance should be reduced in the same amount of computing time.
The implementation of scoring is independent from the implementation of the variance reduction. However they share common concepts. Scoring and variance reduction apply to particle types chosen by the user.
Note
Currently only neutral particles may be scored and/or importance sampled.
Only field free geometries may be used.
Examples on how to use scoring, importance sampling and weight roulette may be found in examples/extended/biasing.
Table of Contents
The kind of scoring referred to in this note and the variance reduction techniques apply to spatial cells given by the user.
The cells may be defined in two kinds of geometries:
It is possible to utilize several parallel geometries in addition to the mass geometry. This provides the user with a lot of flexibility to define separate geometries for different particle types in order to apply scoring or/and variance reduction.
The world volume of the parallel geometry must overlap the world volume of the mass geometry.
Particles crossing a boundary in the parallel geometry where there is vacuum in the mass geometry are also biased. This may be optimized in later versions.
Mass and parallel geometry boundaries are not coincident in the current implementation.
Table of Contents
- 4.1. Introduction
- 4.2. Sampler interface
- 4.3. Concrete sampler classes
Samplers are higher level tools to do the necessary changes of the Geant4 sampling in order to apply importance sampling and weight roulette. The samplers may also be used to apply scoring.
Scoring and variance reduction may be combined arbitrarily for chosen particle types and may be applied to the mass or to parallel geometries. The samplers support all combinations.
Different samplers are implemented for the mass and parallel geometries. Both implement the interface G4VSampler. G4VSampler allows to prepare the combination of scoring and variance reduction chosen and to configure the sampling appropriately. To this end G4VSampler provides Prepare... methods and a Configure:
class G4VSampler {
public:
virtual ~G4VSampler() {}
virtual void PrepareScoring(G4VScorer *Scorer) = 0;
virtual void PrepareImportanceSampling(G4VIStore *istore,
const G4VImportanceAlgorithm
*ialg = 0) = 0;
virtual void PrepareWeightRoulett(G4double wsurvive = 0.5,
G4double wlimit = 0.25,
G4double isource = 1) = 0;
virtual void PrepareWeightWindow(G4VWeightWindowStore *wwstore,
G4VWeightWindowAlgorithm *wwAlg = 0,
G4PlaceOfAction placeOfAction =
onBoundary) = 0;
virtual void Configure() = 0;
virtual void ClearSampling() = 0;
virtual G4bool IsConfigured() const = 0;
};
The methods for setting up the wished combination need specific information:
Scoring: message PrepareScoring with a G4VScorer (see Scoring)
Importance sampling: message PrepareImportanceSampling with a G4VIStore (see Importance sampling) and optionally a G4VImportanceAlgorithm
Weight roulette: message PrepareWeightRoulett with the optional parameters:
wsurvive: survival weight
wlimit: minimal allowed value of weight * source importance / cell importance
isource: importance of the source cell
Weight window: message PrepareWeightWindow with the arguments:
*wwstore: a G4VWeightWindowStore for retrieving the lower weight bounds for the energy-space cells
*wwAlg: a G4VWeightWindowAlgorithm if a customized algorithm should be used
placeOfAction: a G4PlaceOfAction specifying where to perform the biasing
Each object of a sampler class is responsible for one particle type. The particle type is given to the constructor of the sampler classes via the particle type name e.g. "neutron". Dependent on the specific purpose the Configure of a sampler will setup specialized processes (derived from G4VProcess) for transportation in the parallel geometry, scoring, importance sampling and weight roulette for the given particle type. When Configure is invoked the sampler places the processes in the correct order independent of the order in which user invoked the Prepare... methods.
Note
The Prepare... functions may each only be invoked once.
To configure the sampling the function Configure has to be called after the G4RunManager has been initialized.
Two classes implementing the interface G4VSampler: are provided for the mass and a parallel geometry respectively:
G4MassGeometrySampler
G4ParallelGeometrySampler
The constructors of both classes take the particle type name (e.g. "neutron") as argument. The constructor of G4ParallelGeometrySampler in addition needs a reference to the physical world volume of the parallel geometry.
Table of Contents
- 5.1. Introduction
- 5.2. The scoring framework
- 5.3. Standard scoring
- 5.4. Advices for scoring
This chapter describes the Geant4 framework for scoring and a scoring standard implementation.
Two more ways to retrieve information about physical quantities in addition to using Geant4's sensible detectors will be supported by Geant4: scoring and tallying.
Scoring aims to estimate quantities mainly interesting in connection with importance sampling. The values obtainable serve checking the importance sampling. In the standard implementation no errors will be given on this numbers.
Tallying should estimate physical quantities and provide information about the validity of the estimation such as errors. It should also be possible to bin the quantities with respect to several variables and to obtain statistical checks. Tallies are not implemented yet.
Scoring is provided by a framework. It is done particle type wise. Nevertheless it is also possible to score particles of different types into the same scores. The framework may also be easily used for customized scoring.
Scoring may be applied to the mass or a parallel geometry. It is done with an object generically called scorer using a sampler described above. The scorer receives the information about every step a particle of chosen type takes. The information consists of an object of the Geant4 kernel class G4Step and an object of the class G4GeometryCellStep provided in particular for the purpose of scoring and importance sampling. G4GeometryCellStep provides information about the previous and current "cell" of the particles track.
A "scorer" class derives from the interface G4VScorer. Users may create customized "scorers" or use the standard scoring described in Section 5.3.
Classes involved in the framework:
Classes derived from G4VScorer may use the Geant4 framework for scoring. This is the minimum dependence a customized scoring has to have to use the scoring frame. The frame will provide a process messaging a scorer derived from G4VScorer and classes for the setup.
In particular an object of this type may be given to a G4VSampler;. In order to score different particle types in one object of G4VScorer the object may be given to different sampler objects.
The interface:
class G4VScorer { public: virtual ~G4VScorer(){} virtual void Score(const G4Step &step, const G4GeometryCellStep &gstep) = 0; };The member function Score(const G4Step &step, const G4GeometryCellStep &gstep) is invoked for every "PostStep" of a chosen particle before the "PostStepDoIt"-functions of the physical processes are invoked.
- G4GeometryCellStep:
class G4GeometryCellStep { public: // with description G4GeometryCellStep(const G4GeometryCell &preCell, const G4GeometryCell &postCell); // initialise pre and post G4GeometryCell ~G4GeometryCellStep(); const G4GeometryCell &GetPreGeometryCell() const; // addressing the "cell" the track previously touched const G4GeometryCell &GetPostGeometryCell() const; // addressing the current "cell" G4bool GetCrossBoundary() const; // returns true if step crosses boundary of the geometry it refers to // the following functions are used by the scoring and importance // system to set the cell information. void SetPreGeometryCell(const G4GeometryCell &preCell); void SetPostGeometryCell(const G4GeometryCell &postCell); void SetCrossBoundary(G4bool b); };The classes and functions used in G4GeometryCellStep:
G4GeometryCell() identifies a "cell" as a physical volume with a replica number. The "cell" is in the "parallel" geometry if a sampler for "parallel" geometries is used else it is in the mass geometry.
GetPreGeometryCell() returns the previous "cell" the particle touched, or it is equal to GetPostGeometryCell if the track has not crossed a boundary.
GetPostGeometryCell() refers to the current "cell".
GetCrossBoundary() returns "true" in case the particle crosses a boundary in the parallel or mass geometry with respect to the sampler used.
Note
When scoring is done in a "parallel" geometry special action has to be taken to prevent counting of "collisions" with boundaries of the mass geometry as interactions. This is handled differently when scoring is done in the mass geometry.
This chapter describes the standard scoring supported by Geant4. It uses the framework for scoring described above. A customized scoring may be independent from the standard implementation or use or extend parts of the standard implementation. This way a customized scoring may for example provide errors for the estimates or a histogram containing the distribution of the estimator (see examples/extended/biasing).
All the values are scored per cell.
Some standard scores are calculated from the following raw scores:
"D": step length between previous and post step point.
"WD": weight of the particle at the previous step point times the step length.
"WDT": WD divided by the velocity of the particle at the previous step point.
"WDE": weight times energy (both from previous step point) times step length.
"WTE": WDE divided by the velocity of the particle at the previous step point.
The list of scores:
"Importance":
The importance of the cell.
"Tr.Entering"
The sum of tracks entering. Reentrant tracks are counted again..
"Population"
The number of tracks entering and created in a cell. Reentrant tracks are not counted again.
"Collisions"
Number of collisions. Faked collisions with boundaries of the mass geometry are rejected but collisions in other parallel geometries that might exist are counted, wrongly, as collisions.
"Coll*WGT"
Weighted sum of collisions. The weight of the particle when it is just entering the collision, at the post step point.
"NumWGTedE"
The number weighted energy: (Sum of WTE) / (Sum of WDT).
"FluxWGTedE"
The flux weighted energy: (Sum of WDE) / (Sum of WD).
"Av.Tr.WGT"
Average track weight: Importance * (Sum of WD)/(Sum of D).
To use the scoring framework an object only needs to conform to the interface G4VScorer. The standard scoring provides a scorer of this kind using an additional concept of scorer responsible only for one cell: a cell scorer. The calculation of the actual scores is factored out of the cell scorer and the final result is delivered by the cell scorer in a simple struct.
To use the cell scorers additional concepts are needed: the mapping of the cell scorers to the cells, the selection of the cell scorer according to the cell being hit, a table of the final results for a print out and the processes and samplers described in Chapter 4
The concepts of the standard scoring are reflected in the following classes.
All the classes below which are developed for the standard scoring may also be used optionally for a customized scoring,
This is an interface for a scorer responsible for one cell of the geometry. The cell may be in the mass or in a parallel geometry.
A concrete class implementing the interface G4VCellScorer. This is the top level class responsible for the standard scoring for one cell.
This interface describes a store for G4VCellScorer objects. Objects with this type may have their stored G4VCellScorer objects messaged for scoring by an object of the class G4CellStoreScorer.
A concrete class implementing the interface G4VCellScorerStore. Objects of this class create and store G4CellScorer objects.
The user may chose to have a G4CellScorer object created for every cell that gets hit or to create the G4CellScorer object only for certain cells and give pointers of them to the store.
This concrete class is a G4VScorer messaging G4VCellScorer objects obtained from a G4VCellScorerStore.
This concrete class is a G4VScorer and a wrapper around G4CellStoreScorer using a G4CellScorerStore in the mode that it creates a G4CellScorer for every hit cell.
This concrete top level class provides a simple way to do standard scoring for all cells in a geometry.
This class may be used to create a table of standard scores per element of a map (G4MapGeometryCellCellScorer) of G4GeometryCell, G4CellScorer pairs. An instance of such a map is provided by G4CellStoreScorer and G4Scorer.
This class is used to calculate several scores listed in Section 5.3.1 related to the step length.
Objects of this kind contain the scores listed in Section 5.3.1. An object may be retrieved from G4CellScorer.
The G4CellStoreScorer uses this class to store G4CellScorer objects and the G4ScoreTable reads this map to print a table of the scores.
This class is used by G4CellScorer to get the information if a track has been already seen in a cell in the current event. This information is needed for the "Population" score.
The following class diagrams show the relations of the above classes:
Don't choose a GeometryCell that has a boundaries coinciding with the world volume! In the current implementation tracks would be killed when they move outside the world volume before scoring is applied.
When scoring is done in a scoring in a parallel geometry special action has to be taken to prevent counting of "collisions" with boundaries of the tracking geometry as interactions. This is done in the standard implementations $G4CellSCorer; and G4Scorer.
Table of Contents
The importance sampling acts on particles crossing boundaries between "importance cells". The action taken depends on the importance values assigned to the cells. In general a particle history is split or Russian roulette is played if the importance increases or decreases respectively. A weight assigned to the history is changed according to the action taken.
The tools provided for importance sampling require the user to have a good understanding of the physics in the problem. This is because the user has to decide which particle types have to be importance sampled, define the cells and assign importance values to that cells. If this is not done properly it can not be expected that the results describe a real experiment.
The assignment of importance values to a cell is done using an importance store described in the next section. A description of how to specify a customized algorithm for importance sampling and the default algorithm are described in the sections Section 6.4 and Section 6.5.
An "importance store" with the interface G4VIStore is used to store importance values related to cells. In order to do importance sampling the user has to create an object (e.g. of class G4IStore) of type G4VIStore. The samplers may be given a G4VIStore. The user fills the store with cells and their importance values.
A importance store has to be constructed with a reference to the world volume of the geometry used for importance sampling. This may be the world volume of the mass or of a parallel geometry. Importance stores derive from: the interface G4VIStore:
class G4VIStore {
public:
G4VIStore(G4VPhysicalVolume &worldVolume){}
virtual ~G4VIStore(){}
virtual G4double GetImportance(const G4GeometryCell &gCell) const = 0;
virtual G4bool IsKnown(const G4GeometryCell &gCell) const = 0;
virtual G4VPhysicalVolume &GetWorldVolume() = 0;
};
A concrete implementation of an importance store is provided by the class G4VStore. The public part of the class is:
class G4IStore : public G4VIStore
{
public: // with description
explicit G4IStore(const G4VPhysicalVolume &worldvolume);
// initialise the importance store for the given geometry
virtual ~G4IStore();
// destruct
virtual G4double GetImportance(const G4GeometryCell &gCell) const;
// derive a importance value of a "cell" addressed by a G4GeometryCell
// from the store.
virtual G4bool IsKnown(const G4GeometryCell &gCell) const;
// returns true if the gCell is in the store, else false
virtual const G4VPhysicalVolume &GetWorldVolume() const;
// return a reference to the world volume of the
// "importance" geometry
void AddImportanceGeometryCell(G4double importance,
const G4GeometryCell &gCell);
void AddImportanceGeometryCell(G4double importance,
const G4VPhysicalVolume &,
G4int aRepNum = 0);
// Add a "cell" together with a importance value to the store.
void ChangeImportance(G4double importance,
const G4GeometryCell &gCell);
void ChangeImportance(G4double importance,
const G4VPhysicalVolume &,
G4int aRepNum = 0);
// Change a importance value of a "cell".
G4double GetImportance(const G4VPhysicalVolume &,
G4int aRepNum = 0) const ;
...
};
The member function AddImportanceGeometryCell adds a cell together with a importance value to the importance store. The importance values may be returned either according to a physical volume and a replica number or according to a G4GeometryCell. The user has to be aware of the interpretation Section 6.3 of assigning importance values to a cell.
Note
An importance value has to be assigned to every cell.
In Geant4 the world volume has the replica number -1.
A diagram showing how the importance values are assigned: Setting importance values
The different cases:
Cell is not in store
Not filling a certain cell into the store will cause an exception.
Importance value = zero
Tracks of the chosen particle type will be killed.
importance values > 0
Normal allowed values
Importance value smaller zero
Not allowed!
The importance sampling supports using a customized importance sampling algorithm. To this end the sampler interface G4VSampler may be given a pointer to the interface G4VImportanceAlgorithm:
class G4VImportanceAlgorithm
{
public:
virtual ~G4VImportanceAlgorithm() {}
virtual G4Nsplit_Weight Calculate(G4double ipre,
G4double ipost,
G4double init_w) const = 0;
};
The method Calculate takes the arguments:
ipre, ipost: are the importance of the previous cell and the importance of the current cell respectively.
init_w: the particles weight
It returns the struct:
struct G4Nsplit_Weight
{
G4int fN;
G4double fW;
};
fN: the calculated number of particles to exit the importance sampling
fW: the weight of the particles
The user may have a customized algorithm used by providing a class inheriting from G4VImportanceAlgorithm
If no customized algorithm is given to the sampler the default importance sampling algorithm is used. This algorithm is implemented in G4ImportanceAlgorithm.
The default algorithm implements the so called expected value splitting:
When crossing from cell "m" with importance "Im" to cell "n" with importance "In" calculate "r=In/Im". If:
r = 1: continue tracking
r < 1: play Russian roulette with probability for killing the track"pk=1-r"
r > 1: split into "r" track, if "r" is an integer
After splitting the particles will get the new weight w_new = init_w * 1/r.
Importance values may be real numbers. If "r" is not an integer the algorithm for case "r > 1" is:
Two values "n" for the number of particles after splitting are chosen with different probabilities:
n = int(r)+1: with probability: "p = r-int(r)"
n = int(r): with the probability: "1+int(r)-r"
Table of Contents
The weight window technique is a weight based alternative to importance sampling:
apply splitting and Russian roulette dependent on space (cells) and energy
user defines weight windows in contrast to defining importance values as in importance sampling
In contrast to importance sampling this technique is not weight blind. Instead the technique is applied according to the particle weight with respect to the current energy-space cell.
Therefore the technique is convenient to apply in combination with other variance reduction techniques like e.g.cross-section biasing and implicit capture.
A weight window can be specified for every cell and for several energy regions: space-energy cell.
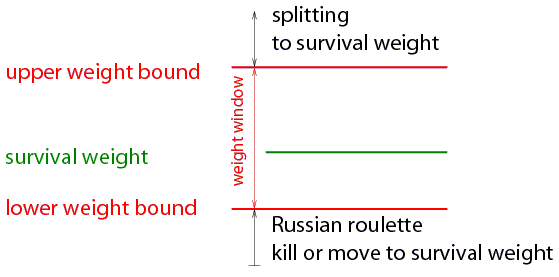 |
Weight window concept
The user specifies a lower weight bound W_L for every space-energy cell.
The upper weight bound W_U and the survival weight W_S are calculated as:
W_U = C_U W_L
and
W_S = C_S W_L.
The user specifies C_S and C_U once for the whole problem.
The user may give different sets of energy bounds for every cell or one set for all geometrical cells
Special case: if C_S = C_U = 1 for all energies than weight window is equivalent to importance sampling
The user can chose to apply the technique: on boundaries, on collisions or on boundaries and collisions
The energy-space cells are realized by G4GeometryCell as in importance sampling. The cells are stored in an weight window store defined by G4VWeightWindowStore:
class G4VWeightWindowStore {
public:
G4VWeightWindowStore();
virtual ~G4VWeightWindowStore();
virtual G4double GetLowerWeitgh(const G4GeometryCell &gCell,
G4double partEnergy) const = 0;
virtual G4bool IsKnown(const G4GeometryCell &gCell) const = 0;
virtual const G4VPhysicalVolume &GetWorldVolume() const = 0;
};
A concrete implementation is provided:
class G4WeightWindowStore: public G4VWeightWindowStore {
public:
explicit G4WeightWindowStore(const G4VPhysicalVolume &worldvolume);
virtual ~G4WeightWindowStore();
virtual G4double GetLowerWeitgh(const G4GeometryCell &gCell,
G4double partEnergy) const;
virtual G4bool IsKnown(const G4GeometryCell &gCell) const;
virtual const G4VPhysicalVolume &GetWorldVolume() const;
void AddLowerWeights(const G4GeometryCell &gCell,
const std::vector<G4double> &lowerWeights);
void AddUpperEboundLowerWeightPairs(const G4GeometryCell &gCell,
const G4UpperEnergyToLowerWeightMap&
enWeMap);
void SetGeneralUpperEnergyBounds(const
std::set<G4double, std::less<G4double> > & enBounds);
private::
...
};
The user may chose equal energy bounds for all cells. In this case a set of upper energy bounds have to be given to the store using the method SetGeneralUpperEnergyBounds. If a general set of energy bounds have been set the AddLowerWeights can be used to add the cells.
Alternative the user may chose different energy regions for different cells. In this case the user has to give a map of upper energy bounds to lower weight bounds for every cell using the method AddUpperEboundLowerWeightPairs.
Weight window algorithms implementing the interface class G4VWeightWindowAlgorithm can be used to define a customized algorithm:
class G4VWeightWindowAlgorithm {
public:
G4VWeightWindowAlgorithm();
virtual ~G4VWeightWindowAlgorithm();
virtual G4Nsplit_Weight Calculate(G4double init_w,
G4double lowerWeightBound) const = 0;
};
A concrete implementation is provided and used as default:
class G4WeightWindowAlgorithm : public G4VWeightWindowAlgorithm {
public:
G4WeightWindowAlgorithm(G4double upperLimitFaktor = 5,
G4double survivalFaktor = 3,
G4int maxNumberOfSplits = 5);
virtual ~G4WeightWindowAlgorithm();
virtual G4Nsplit_Weight Calculate(G4double init_w,
G4double lowerWeightBound) const;
private:
...
};
The constructor takes three parameters for specifying the factors used in calculating the upper weight bound (upperLimitFaktor), the survival weight (survivalFaktor) and for introducing a maximal number (maxNumberOfSplits) of copies to be created in one go.
The inverse of the maxNumberOfSplits is used in addition to specify the minimum survival probability in case of Russian roulette.
Table of Contents
- 8.1. Introduction
- 8.2. The weight roulette concept
Weight roulette (also called weight cutoff) is usually applied if importance sampling and implicit capture are used together. Implicit capture is not described here only note the following: Implicit capture reduces a particle weight in every collision instead of killing the particle with some probability.
Together with importance sampling the weight of a particle may become so low that it doesn't change any result significantly. So tracking a very low weight particle means wasting computing time. Weight roulette is applied in order to solve this problem.
Weight roulette has to take the importance "Ic" of the current cell and the importance "Is" of the cell the source is located in into account by using the ratio "R=Is/Ic".
Weight roulette uses a relative minimal weight limit and a relative survival weight. When a particle falls below the weight limit Russian roulette is plaid. If the particle survives tracking will be continued and the particle weight will be set to the survival weight.
The weight roulette uses the following parameters with their default values:
wsurvival: 0.5
wlimit: 0.25
isource: 1
The following algorithm is applied:
If a particle weight "w" is lower than R*wlimit:
the weight of the particle will be changed to "ws = wsurvival*R"
the probability for the particle to survive is "p = w/ws"